Reading Results of a Tukeys Post Hoc

• Descriptive Statistics for Subgroups
• ANOVA - Flowchart
• SPSS ANOVA Dialogs
• SPSS ANOVA Output
• SPSS ANOVA - Post Hoc Tests Output
• APA Mode Reporting Post Hoc Tests

Post hoc tests in ANOVA exam if the difference between
each possible pair of means is statistically significant. This tutorial walks you through running and understanding mail service hoc tests using depression.sav, partly shown below.

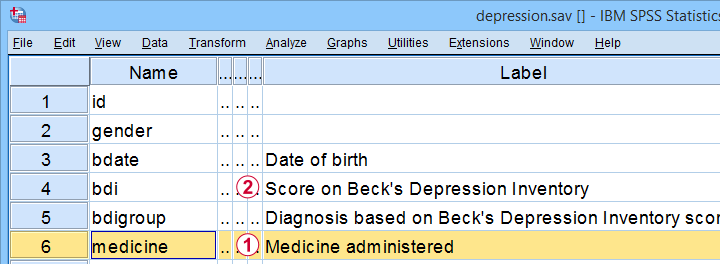
The variables we'll employ are

the medicine that our participants were randomly assigned to and
their levels of depressiveness measured 16 weeks after starting medication.

Our research question is whether some medicines result in lower depression scores than others. A meliorate analysis here would have been ANCOVA but -sadly- no low pretest was administered.

Quick Data Check

Earlier jumping blindly into whatsoever analyses, let'south commencement come across if our data look plausible in the first identify. A adept first footstep is inspecting a histogram which I'll run from the SPSS syntax below.

*QUICK Check DEPENDENT VARIABLE.

frequencies bdi
/format notable
/histogram.

Effect

First off, our histogram (shown beneath) doesn't testify anything surprising or alarming.

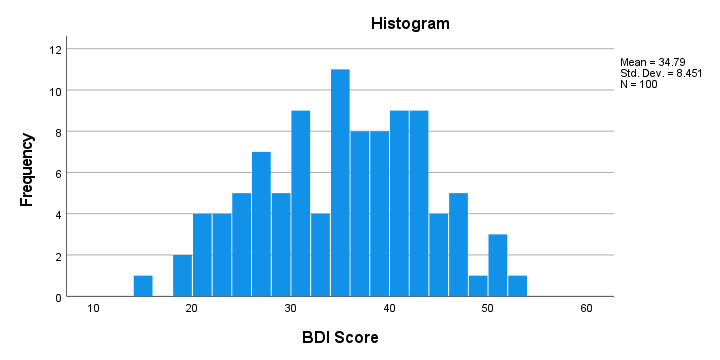
Also, notation that North = 100 and then this variable does not have any missing values. Finally, information technology could be argued that a single participant near fifteen points could be an outlier. It doesn't expect too bad so nosotros'll but exit it for at present.

Descriptive Statistics for Subgroups

Permit's at present run some descriptive statistics for each medicine group separately. The right way for doing and so is from or only typing the 2 lines of syntax shown below.

*DESCRIPTIVE STATISTICS FOR SUBGROUPS OF CASES.

means bdi by medicine
/cells count min max hateful median stddev skew kurt.

Effect

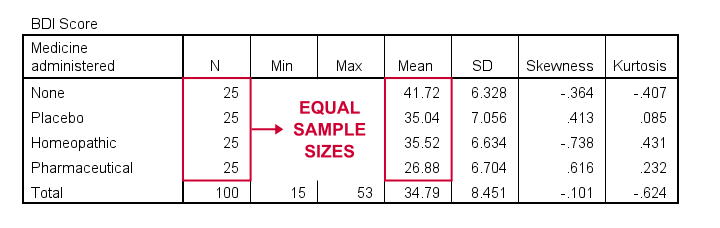
As shown, I similar to nowadays a nicely detailed table including the

• mean,
• median (omitted here),
• standard deviation,
• skewness and
• kurtosis

for each grouping separately. Merely most important here are the sample sizes because these bear on which assumptions we'll need for our ANOVA.

Also note that the hateful depression scores are quite different across medicines. Still, these are based on rather small samples. So the big question is: what can we conclude near the entire populations? That is: all people who'll take these medicines?

ANOVA - Goose egg Hypothesis

In curt, our ANOVA tries to demonstrate that some medicines work better than others past nullifying the contrary claim. This cipher hypothesis states that the population mean depression scores are equal
across all medicines. An ANOVA will tell us if this is credible, given the sample data we're analyzing. Nevertheless, these data must meet a couple of assumptions in social club to trust the ANOVA results.

ANOVA - Assumptions

ANOVA requires the following assumptions:

• independent observations;
• normality: the dependent variable must be normally distributed within each subpopulation we're comparing. However, normality is not needed if each north > 25 or then.
• homogeneity: the variance of the dependent variable must be equal across all subpopulations we're comparison. However, homogeneity is not needed if all sample sizes are roughly equal.

Now, homogeneity is only required for sharply unequal sample sizes. In this case, Levene's examination tin exist used to examine if homogeneity is met. What to practice if it isn't, is covered in SPSS ANOVA - Levene'due south Test "Significant".

ANOVA - Flowchart

The flowchart below summarizes when/how to check the ANOVA assumptions and what to practise if they're violated.

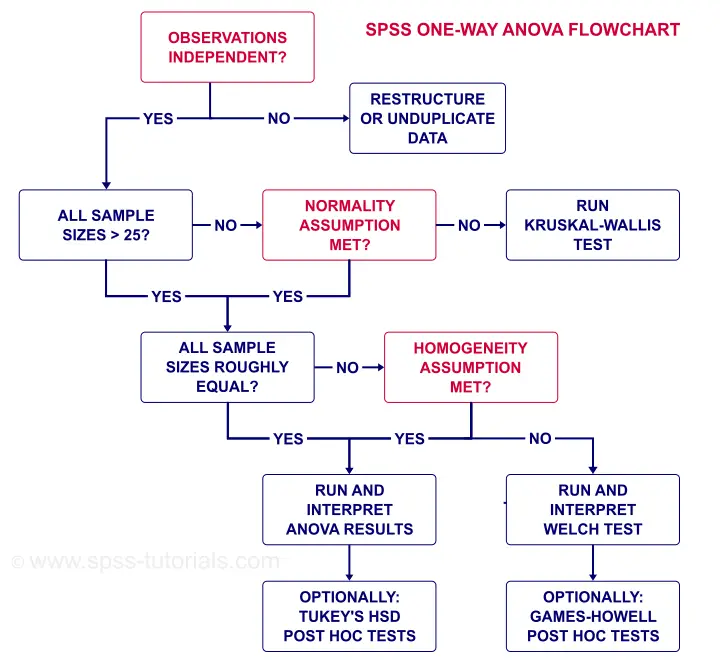
Notation that low.sav contains four medicine samples of n = 25 independent observations. It therefore meets all ANOVA assumptions.

SPSS ANOVA Dialogs

Nosotros'll run our ANOVA from equally shown below.

Adjacent, let'due south fill out the dialogs as shown below.

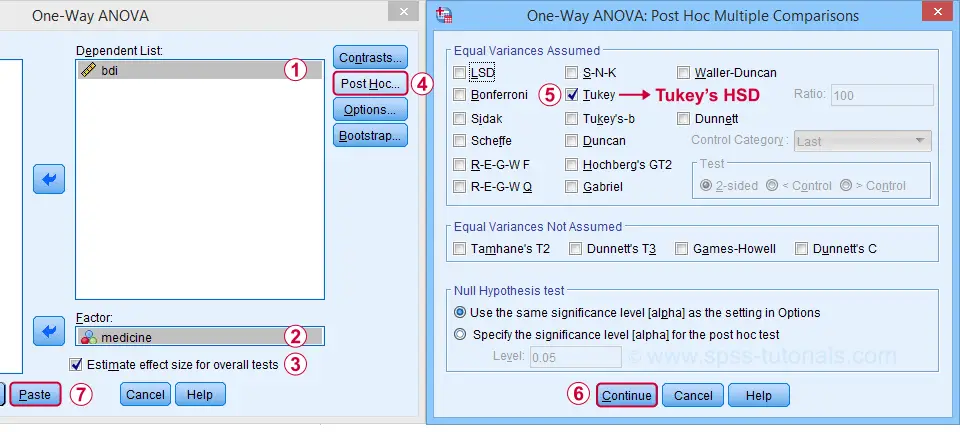
Estimate effect size(...) is only bachelor for SPSS version 27 or higher. If you're on an older version, y'all tin get information technology from ("ANOVA table" nether "Options").

Tukey'southward HSD ("honestly significant difference") is the nearly common post hoc examination for ANOVA. It is listed under "equal variances causeless", which refers to the homogeneity assumption. However, this is not needed for our data because our sample sizes are all equal.

Completing these steps results in the syntax beneath.

*Basic ANOVA Consequence SIZE AND Postal service HOC TESTS.

ONEWAY bdi By medicine
/ES=OVERALL
/MISSING Analysis
/CRITERIA=CILEVEL(0.95)
/POSTHOC=TUKEY ALPHA(0.05).

SPSS ANOVA Output

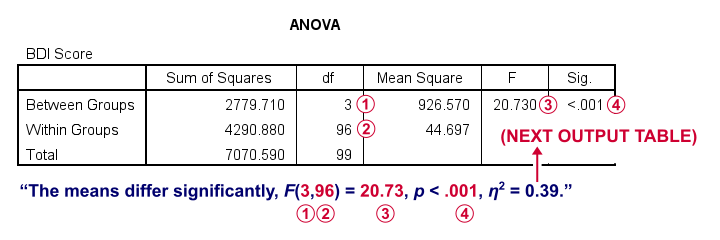
Start off, the ANOVA table shown below addresses the cipher hypothesis that all population means are equal. The significance level indicates that p < .001 then we reject this zilch hypothesis. The figure below illustrates how this result should be reported.

What'south absent from this tabular array, is eta squared, denoted as η ². In SPSS 27 and higher, nosotros find this in the next output table shown below.

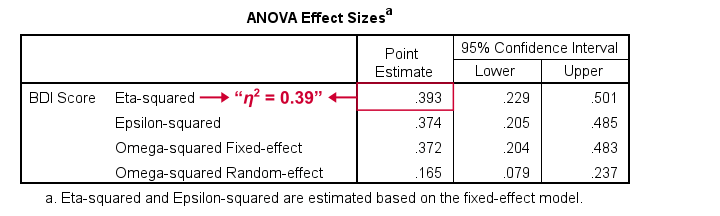
Eta-squared is an upshot size measure: it is a unmarried, standardized number that expresses how different several sample means are (that is, how far they prevarication autonomously). Generally accepted rules of pollex for eta-squared are that

• η ² = 0.01 indicates a small outcome;
• η ^two = 0.06 indicates a medium effect;
• η ² = 0.fourteen indicates a large effect.

For our instance, η ^two = 0.39 is a huge effect: our iv medicines resulted in dramatically different mean low scores.

This may seem to complete our analysis but there's one thing nosotros don't know yet: precisely which mean differs from which mean? This final question is answered by our post hoc tests that we'll discuss next.

SPSS ANOVA - Postal service Hoc Tests Output

The tabular array below shows if the difference between each pair of means is statistically significant. It also includes 95% confidence intervals for these differences.

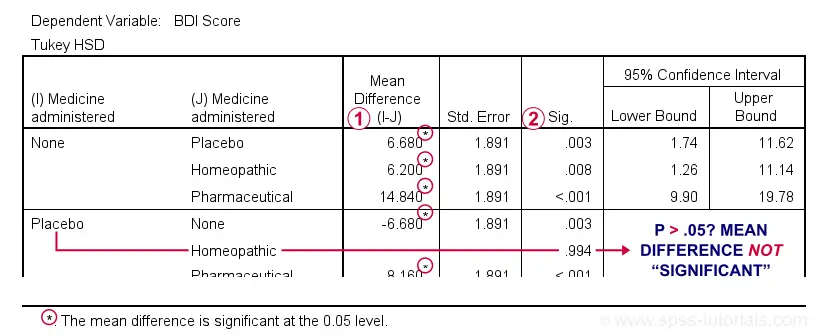
Mean differences that are "significant" at our chosen α = .05 are flagged. Note that each hateful differs from each other mean except for Placebo versus Homeopathic.

If we have a skillful expect at the verbal 2-tailed p-values, we run into that they're all < .01 except for the aforementioned comparison.

Given this last finding, I suggest rerunning our post hoc tests at α = .01 for reconfirming these findings. The syntax below does just that.

*Basic ANOVA WITH ALPHA = 0.01 FOR POST HOC TESTS.

ONEWAY bdi BY medicine
/ES=OVERALL
/MISSING ANALYSIS
/CRITERIA=CILEVEL(0.95)
/POSTHOC=TUKEY Blastoff(0.01).

APA Way Reporting Postal service Hoc Tests

The table below shows how to report mail hoc tests in APA manner.

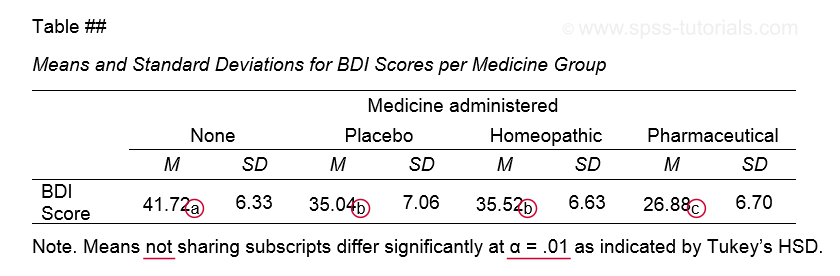
This table itself was created with a MEANS command like we used for Descriptive Statistics for Subgroups. The subscripts are based on the Homogeneous Subsets table in our ANOVA output.

Note that nosotros chose α = .01 instead of the usual α = .05. This is but more informative for our case assay considering all of our p-values < .05 are also < .01.

This APA table also seems available from but I don't recommend this: the p-values from Custom Tables seem to be based on Bonferroni adjusted contained samples t-tests instead of Tukey'south HSD. The general stance on this is that this procedure is overly bourgeois.

Concluding Notes

Right, and so a common routine for ANOVA with mail service hoc tests is

1. run a basic ANOVA to run into if the population means are all equal. This is ofttimes referred to as the jitney test (omnibus is Latin, pregnant something like "nigh all things");
2. only if nosotros reject this overall null hypothesis, then notice out precisely which pairs of ways differ with postal service hoc tests (postal service hoc is Latin for "later on that").

Running post hoc tests when the omnibus examination is non statistically meaning is generally frowned upon. Some scenarios could perhaps justify doing so only let'southward leave that discussion for another twenty-four hour period.

Right, so that should do. I promise yous found this tutorial helpful. If you've whatever questions or remarks, delight throw me a comment below. Other than that...

cheers for reading!

THIS WEBSITE USES COOKIES

.

Reading Results of a Tukeys Post Hoc

Source: https://www.spss-tutorials.com/spss-one-way-anova-with-post-hoc-tests-example/

Share this post